
Nikolaj Bogdanov-Belskij: Устный счёт. В народной школе С. А. Рачинского, "Huvudräkning. I S. A. Rakinskijs folkskola." (1895).
Jag hade aldrig sett denna tavla innan jag stötte på den på nätet häromdagen. Den blev mycket snart en av mina absoluta favoriter, av flera anledningar. Såväl helhet som detaljer - näverskor, att läraren Rakinskij är en faktisk person med en intressant historia, med mera - och så naturligtvis att där finns ett fint problem inlagt, som kan göra betraktaren lika förbryllad som skolpojkarna.
Högre upplösning här
Till själva problemet:
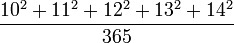
Det kan förvisso förenklas på flera sätt. Jag redogör för den metod jag fastnade för.
Att det går att lösa i huvudet, alltså någorlunda enkelt, är en viktig ledtråd.
Kvadraterna på så här låga tal kan man gärna ha klara i huvudet (om inte, öva): 100, 121, 144, 169, 196. Att summera dem är inte lika enkelt. Men om man börjar med ett överslag, att genomsnittet är ungefär mittemellan 100 och 196, eller säg 150 högt räknat. 5 gånger 150 blir 750, alltså en bit över de 730 som ju är dubbelt så mycket som 365. Så om svaret skall vara enkelt så borde två passa?
Wikipedia (eng.): Nikolay Bogdanov-Belsky
Wikipedia (ryska): Устный счёт. В народной школе С. А. Рачинского
4 kommentarer:
Inte för att ni måste hålla med :-) när frågan ställdes gavs några förslag på lösningar som är lite mer krävande och betydligt exaktare än ovanstående förhoppningsfulla höftande.
Faktoiders lördagsfråga: Huvudräkning
Om man ger informationen att det skall vara ett heltal är detta en utmärkt övning i matematiskt resonemang. Men 1895 undrar jag om frågan ställdes på det sättet, speciellt med tanke på de stackars elevernas förskräckta ansiktsuttryck. Snarare en övning i att hålla alla dessa intermediära beräkningar i huvudet...
I vilket fall jag vidhåller att 10^2+(10+1)^2+...
ät lättare eftersom det ger en split i hundratal.
Jag vet inte hur Rakinskij lade fram problemet. Men däremot gjorde jag det. :-)
Eleverna ja; kolla grabben t.v., ser han inte ut som en som knäckt problemet? Möjligen även han som viskar i lärarens öra. De som står vid tavlan verkar dock betydligt mer avspända än de två i förgrunden.
Att man kan lägga undan de jämna hundratalen förenklar onekligen, bra poäng.
Tavlan är helt underbar! Fastnar i alla de olika uttrycken i kroppsspåk osv.
Skicka en kommentar